Accelerate MATLAB with Python and Numba
Part 11 of the Python Is The Ultimate MATLAB Toolbox series.
Upper panel: flow computed with MATLAB 2022b using code by Jamie Johns.
Lower panel: flow computed with MATLAB 2022b calling the same Navier-Stokes solver translated to Python with Numba. It repeats the simulation more than three times in the amount of time it takes the MATLAB-only solver to do this once.
Introduction
MATLAB’s number crunching power is impressive. If you’re working with a compute-bound application though, you probably want it to run even faster. After you’ve exhausted the obvious speed enhancements like using more efficient algorithms, vectorizing all operations, and running on faster hardware, your last hope may be to to rewrite the slow parts in a compiled language linked to MATLAB through mex. This is no easy task though. Re-implementing a MATLAB function in C++, Fortran, or Java is tedious at best, and completley impractical at worst if the code to be rewritten calls complex MATLAB or Toolbox functions.
Python and Numba are an alternative to mex
In this article I show how Python and Numba can greatly improve MATLAB performance with less effort, and with greater flexibility, than using mex with C++, Fortran, or Java. You’ll need to include Python in your MATLAB workflow, but that’s no more difficult than installing compilers and configuring mex build environments.
Two examples demonstrate the performance boost Python and Numba can bring MATLAB: a simple Mandelbrot set computation, and a much more involved Navier-Stokes solver for incompressible fluid flow. In both cases, the Python augmentation makes the MATLAB application run several times faster.
- Python+Numba as an alternative to mex
- What is Numba?
- Hardware, OS details
- Example 1: Mandelbrot set
- Example 2: incompressible fluid flow
Python+Numba as an alternative to mex
The mex compiler front-end enables the creation of functions written in C, C++, Fortran, Java, and .Net that can be called directly from MATLAB. To use it effectively, you’ll need to be proficient in one of these languages and have a supported compiler. With those in place, the fastest way to begin writing a mex-compiled function is to start with existing working code such as any of the MathWorks' mex examples and modifying it to your needs.
A big challenge to translating MATLAB code is that one line of MATLAB can translate to dozens of lines in a compiled language. Standard MATLAB statements such as
y = max((A\b)*v',[],'all');become a logistical headache in the compiled languages.
Do you have access to an optimized linear algebra library?
Do you know how to set up the calling arguments?
What if the inputs are complex?
What if A is rectangular?
It is not straightforward.
Python, on the otherhand, can often match MATLAB expressions one-to-one (although the Python expressions are usually longer). The Python version of the line above is
Python:
y = np.max((np.linalg.solve(A,b).dot(v.T))where np. is the prefix for the NumPy module.
If you’re familiar with Python and its ecosystem of numeric and scientific modules, you’ll be able to translate a MATLAB function to Python much faster than you can translate MATLAB to any compiled language.
For the most part, numerically intensive codes run at comparable speeds in MATLAB and Python. Simply translating MATLAB to Python will rarely give you a worthwhile performance boost. To see real acceleration you’ll need to additionally use a Python code compiler such as Cython, Pythran, f2py, or Numba.
Numba offers the most bang for the buck—the greatest performance for the least amount of effort—and is the focus of this post.
What is Numba?
From the Numba project’s Overview:
Numba is a compiler for Python array and numerical functions that gives you the power to speed up your applications with high performance functions written directly in Python.
Numba generates optimized machine code from pure Python code using the LLVM compiler infrastructure. With a few simple annotations, array-oriented and math-heavy Python code can be just-in-time optimized to performance similar as C, C++ and Fortran, without having to switch languages or Python interpreters.
Type casting Python function arguments
Three steps are needed to turn a conventional Python function into a much faster Numba-compiled function:
- Import the
jitfunction and all data types you plan to use from the Numba module. Also import theprangefunction if you plan to run for loops in parallel. - Precede your function definition with
@jit() - Pass to
@jit()type declarations for of each input argument and return value
The steps are illustrated below
with a simple function that accepts a 2D array
of 32 bit floating point numbers and a 64 bit floating point
tolerance, then
returns an unsigned 64 bit integer containing the count of
terms in the array that are less than the tolerance.
We’ll ignore the fact that this is a simple operation
in both MATLAB (sum(A < tol)) and Python (np.sum(A < tol)).)
First the plain Python version:
Python:
def n_below(A, tol):
count = 0
nR, nC = A.shape
for r in range(nR):
for c in range(nC):
if A[r,c] < tol:
count += 1
return countNow with Numba:
Python:
|
|
Only the two highlighted lines were added; the body of the function did not change. Let’s see what this buys us:
In : A = np.random.rand(2000,3000).astype(np.float32)
In : tol = 0.5
In : %timeit n_below(A, tol) # conventional Python
11.3 s ± 72.3 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
In : %timeit n_below_numba(A, tol) # Python+Numba
9.92 ms ± 251 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Time dropped from 11.3 seconds to 9.92 milliseconds, a factor of more than 1,000. While this probably says more about how slow Python 3.8 is for this problem1, the Numba version is impressive. It is in fact even a bit faster than the native NumPy version:
In : %timeit np.sum(A < tol)
10.2 ms ± 193 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)For completeness, MATLAB 2022b does this about as quickly as NumPy:
>> A = single(rand(2000,3000));
>> tol = 0.5;
>> tic; sum(A < tol); tocRepeating the last line a few times gives a peak (that is, minimum) time of 0.011850 seconds (11.85 ms).
Options
The @jit() decorator has a number of options that affect how
Python code is compiled. All four of the options
below appear on every @jit() instance in the Navier-Stokes
code. Here’s an example:
@jit(float64[:,:](float64[:,:], float64),
nopython=True, fastmath=True, parallel=True, cache=True)
def DX2(a,dn):
# finite difference for Laplace of operator in two dimensions
# (second deriv x + second deriv ystaggered grid)
return (a[:-2,1:-1] + a[2:,1:-1] + a[1:-1,2:] + a[1:-1,:-2] -
4*a[1:-1,1:-1])/(dn**2)nopython=True
Numba compiled functions can work either in object mode, where
the code can interact with the Python interpreter, or in nopython
mode where the Python interpeter is not used. nopython mode
excludes the Python interpreter and results in higher performance.
fastmath=True
This option matches the -Ofast optimization switch
used by compilers in the
Gnu Compiler Collection. It allows the compiler to
resequence floating point computations in a non IEEE 754
compliant manner—enabling significant speed increases
at the risk of generating incorrect (!) results.
To use this option with confidence, compare solutions produced with and without it. Obviously if the results differ appreciably you shouldn’t use this option.
parallel=True
This option tells Numba to attempt automatic parallelization of
code blocks in jit compiled functions. Parallelization may
be possible even
if these functions do not explicitly call the prange() to
make a for loop run in parallel.
Let’s try this out on the simple n_below() function
shown above:
Python:
from numba import jit, prange, uint64, float32, float64
@jit(uint64(float32[:,:], float64), nopython=True, parallel=True)
def n_below_parallel(A, tol):
count = 0
nR, nC = A.shape
for r in prange(nR): # <- parallel for loop
for c in range(nC):
if A[r,c] < tol:
count += 1
return countBy parallelizing the rows of A over cores I get twice the
performance on my 4 core laptop:
In : %timeit n_below_parallel(A, tol)
5.96 ms ± 299 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Even more impressively,
the Navier-Stokes solver runs nearly 2x more quickly with
parallel=True on my 4 core laptop even though it has no
parallel for loops.
cache=True
A program that includes Numba-enhanced Python functions start more slowly because the jit compiler needs to compile the functions before the program can begin running. The delay is barely noticable with small functions.
That’s not the case for the more complicated jit-compiled
functions in the Navier-Stokes solver. These impose a 10 second
start-up delay on my laptop. The cache=True option tells Numba
to cache the result of its compilations for immediate on
subsequent runs. The code is only recompiled if any of the @jit
decorated functions change.
Hardware, OS details
The examples were run on a 2015 Dell XPS13 laptop with 4 cores of i5-5200U CPU @ 2.2 GHz and 8 GB memory. The OS is Ubuntu 20.04. MATLAB 2022b was used but the code will run with any MATLAB version from 2020b onward.
Anaconda Python 2020.07 with Python 3.8.8 was used to permit running on older versions of MATLAB, specifically 2020b. (Yes, I’m aware Python 3.11 runs more quickly than 3.8. MATLAB does not yet support that version though.)
Example 1: Mandelbrot set
This example comes from the High Performance Computing chapter of my book. There I implement eight versions of code that compute terms of the Mandelbrot set: MATLAB, Python, Python with multiprocessing, Python with Cython, Python with Pythran, Python with f2py, Python with Numba, and finally MATLAB calling the Python/Numba functions.
The baseline MATLAB version is much faster than the baseline Python implementation. However, employing any of the compiler-augmented tools like Cython, Pythran, f2py, or Numba turns the tables and makes the Python solutions much faster than MATLAB.
baseline MATLAB2 :
|
|
baseline Python:
|
|
The Python with Numba version is the same as the baseline Python version with five additional Numba-specific lines. An explanation of each highlighted line appears below the code:
Python with Numba:
|
|
Line 5 imports the necessary items from the numba module:
jit() is a decorator that precedes functions
we want Numba to compile. prange() is a parallel version of
the Python range() function. It turns regular for loops into
parallel for loops where work is automatically distributed
over the cores of your computer.
The remaining items from uint8 to complex128 define data
types that will be employed in function signatures.
Line 6 defines the signature of the nIter() function
as taking a complex scalar and 64 bit integer as inputs
and returning an unsigned 8 bit integer.
(The remaining keyword arguments like nopython= were explained above.)
Lines 15 and 16 define the signature of the MB() function
as taking a pair of 1D double precision arrays and a scalar 64 integer
and returning a 2D array of unsigned 8 bit integers.
Line 21 implements a parallel for loop; iterations for
different values of i are distributed over the cores.
What have we gained with the five extra Numba lines? This table shows how our three codes perform for different image sizes; times are in seconds.
| N | MATLAB 2022b | Python 3.8.8 | Python 3.8.8 + Numba |
|---|---|---|---|
| 500 | 0.70 | 8.22 | 0.04 |
| 1000 | 2.29 | 32.70 | 0.14 |
| 2000 | 9.04 | 127.84 | 0.61 |
| 5000 | 56.77 | 795.41 | 3.51 |
The Python+Numba performance borders on the unbelievable—but don’t take my word for it, run the three implementations yourself!
One “cheat” the Python+Numba solution enjoys is that its parallel
for loop takes advantage of the four cores on my laptop.
I tried
MATLAB’s parfor parallel for loop construct but, inexplicably,
it runs slower than a conventional sequential for loop. Evidently
multiple cores are only used if you have a license for
the Parallel Computing Toolbox (which I don’t).
MATLAB + Python + Numba
If Python can run faster with Numba, MATLAB can too. All we need
to do is import the MB_numba module and call its
jit-compiled MB() function from MATLAB:
MATLAB:
|
|
MB() from MB_numba.py
is a Python function so it returns a Python result.
To make the benchmark against the baseline
MATLAB version fair, the program includes conversion of the
NumPy img array to a MATLAB matrix (using
py2mat.m)
in the elapsed time.
The table below repeats the MATLAB baseline times from the
previous table. Numeric values in the middle and right column
are elapsed time in seconds.
| N | MATLAB 2022b | MATLAB 2022b + Python 3.8.8 + Numba |
|---|---|---|
| 500 | 0.70 | 0.18 |
| 1000 | 2.29 | 0.17 |
| 2000 | 9.04 | 0.64 |
| 5000 | 56.77 | 3.85 |
Visualizing the result
Call MATLAB’s imshow() or imagesc()
functions on the img matrix
if you want to see what the matrix looks like.
For example,
MATLAB:
|
|
Similarly, in Python:
|
|
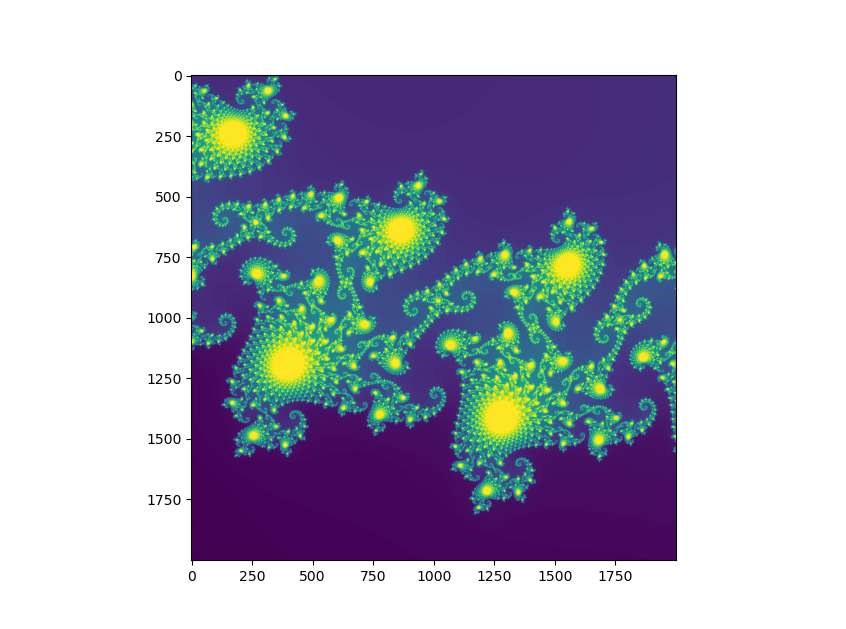
Mandelbrot set image made with matplotlib.
Example 2: incompressible fluid flow
The Mandelbrot example is useful for demonstrating how to use Numba and for giving insight to the performance boosts it can give. But useful as a computational pattern resembling real work? Not so much.
The second example represents computations as might appear in a realistic scientific application. It demonstrates MATLAB+Python+Numba with a two dimensional Navier-Stokes solver for incompressible fluid flow. I chose an implementation by Jamie Johns which shows MATLAB at its peak performance using fully vectorized code. While this code only computes flow in 2D, the sequence of calculations and memory access patterns are representative of scientific and engineering applications. Jamie Johns' YouTube channel has interesting videos produced with his code.
Boundary conditions
A clever aspect of Jamie Johns' code is that boundary conditions are defined graphically. You create an image, for example a PNG, where colors define properties at each grid point: black = boundary, red= outflow (source), and green = inflow (sink). The image borders, if they aren’t already black, also define boundaries.
This PNG image, which can be found in the original code’s
Github repository
as scenario_sphere2.png,
represents flow moving from left to right around a circle,
a canonical fluid dynamics problem I studied as an undergrad:

Of course, if boundary conditions are supplied as images, they can be arbitrarily complex. I recalled an amusing commercial by Maxell, “Blown Away Guy”, from my youth. With a bit of photo editing I converted

to the following boundary conditions image:

The domain dimensions are 15 meters x 3.22 meters and the CFD mesh has 400 x 86 grid points, giving a relatively coarse resolution of 3.7 cm between points. My memory-limited (8 GB) laptop can’t handle a finer mesh.
Initial conditions
- time step: 0.003 seconds
- number of iterations: 12,900
- air density = 1 kg/m$^3$
- dynamic viscosity = 0.001 kg/(m s)
- air speed leaving the speaker: 0.45 m/s
The low air speed is admittedly contrived and certainly lower than the commercial’s video suggests. (my guess is for that is at least 2 m/s). I found the solver fails to converge, then exits with an error, if the flow speed is too high. Same thing for number of iterations—too many and the solver diverges. Trial and error brought me to 0.45 m/s and 12,900 iterations as values that produce the longest animation.
I don’t understand the reason of the failure (mesh too coarse?) and haven’t been motivated to figure out what’s going on. This is, after all, an exercise in performance tweaking rather than studying turbulence or computing coefficients of drag.
Running the code
My modifications to Jamie Johns' MATLAB code and the translation
to Python + Numba can be found at
https://github.com/AlDanial/matlab_with_python/,
under performance/fluid_flow
(MIT license).
The code there can be run three ways:
entirely in MATLAB, entirely in Python, or with
MATLAB calling Python.
One thing to note is that the computational codes are purely batch
programs that write .mat and .npy data files.
No graphics appear.
The flow can be visualized with
a separate post-processing
step after the flow speeds are saved as files.
MATLAB (2020b through 2022b)
Start MATLAB and enter the name of the main program,
Main, at the prompt. I had to start MATLAB with -nojvm
to suppress the GUI (and close all other applications, especially
web browsers) to give the program enough memory.
>> MainPython + Numba
On Linux and macOS, just type ./py_Main.py in a console.
On Windows, open a Python-configured terminal (such as the
Anaconda console) and enter python py_Main.py.
MATLAB + Python + Numba
Edit Main.m and change the value of Run_Python_Solver to true.
Save it, then run Main and the MATLAB prompt.
Operation
Regardless of how you run the code (MATLAB / Python / MATLAB + Python),
the steps of operation are the same: the application creates a subdirectory
called NS_velocity then populates it with .npy files (Python
and MATLAB+Python) or .mat files (pure MATLAB).
These files contain the x and y components of the flow speed at
each grid point for a batch of iterations.
The first time the Python or MATLAB+Python program starts,
expect to see delay of about 30 seconds while Numba compiles the
@jit decorated functions in navier_stokes_functions.py.
This is a one-time cost though; subsequent runs will start
much more quickly.
Performance
MATLAB runs more than three times faster using the Python+Numba
Navier-Stokes solver. More surprisingly, Python without Numba
also runs faster than MATLAB. I updated the performance table
on 2022-10-30 following a LinkedIn post by
Artem Lenksy
asking how the recently released 3.11 version fares on this problem.
Numba is not yet available for 3.11 so I reran without @jit
decorators—and threw in a 3.8.8 run without Numba as well:
| Solver | Elapsed seconds |
|---|---|
| MATLAB 2022b | 458.35 |
| Python 3.11.0 | 238.95 |
| Python 3.8.8 | 237.46 |
| MATLAB 2022b + Python 3.8.8 + Numba | 128.89 |
| Python 3.8.8 + Numba | 126.99 |
Two surprises here: plain Python + NumPy is faster than MATLAB, and Python 3.11.0 is no faster than 3.8.8 for this compute-bound problem.
Visualization
The program animate_navier_stokes.py generates an animation
of flow computed earlier with py_Main.py or Main.m. The most direct
way to use it is by giving it the directory (NS_velocity by
default) containing flow velocity
files and whether you want to see
*.mat files generated by MATLAB (use --matlab)
or *.npy files generated by either Python or the MATLAB+Python combination
(use --python).
(Note: the program loads many Python modules and takes a
long time to start the first time.)
./animate_navier_stokes.py --python NS_velocityWith this command the program first loads all *.npy files
in the NS_velocity
directory, then writes a large
merged file (merged_frames.npy, 1.7 GB)
containing the entire solution in one file. You can later
load the merged file much more quickly than reading
the individual *.npy files.
The first thing you’ll notice is the animation proceeds slowly. To speed things up, skip a few frames. The next command reads from the merged frame file and only shows every 50th frame:
./animate_navier_stokes.py --npy merged_frames.npy --incr 50Use the --png-dir switch to write individual frames to PNG files
in the given directory. For example
./animate_navier_stokes.py --npy merged_frames.npy --png-dir PNG --incr 400will create the directory PNG then populate it with 33 files with
names like PNG/frame_08000.png. I created the video at the
top of this post by saving individual frames, overlaying the Maxell
image on each, then generating an MP4 file with ffmpeg.
Table of Contents | Previous: Symbolic math | Next : Distribute MATLAB Computations To Python Running on a Cluster
-
Python has an impressive performance road-map ahead. ↩︎
-
Mike Croucher at the MathWorks provided code tweaks to improve the performance of this implementation. ↩︎
